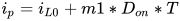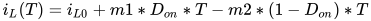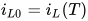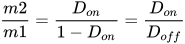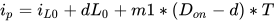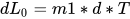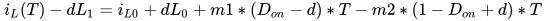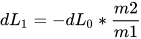开关电源的阻尼振荡

Buck振荡波形

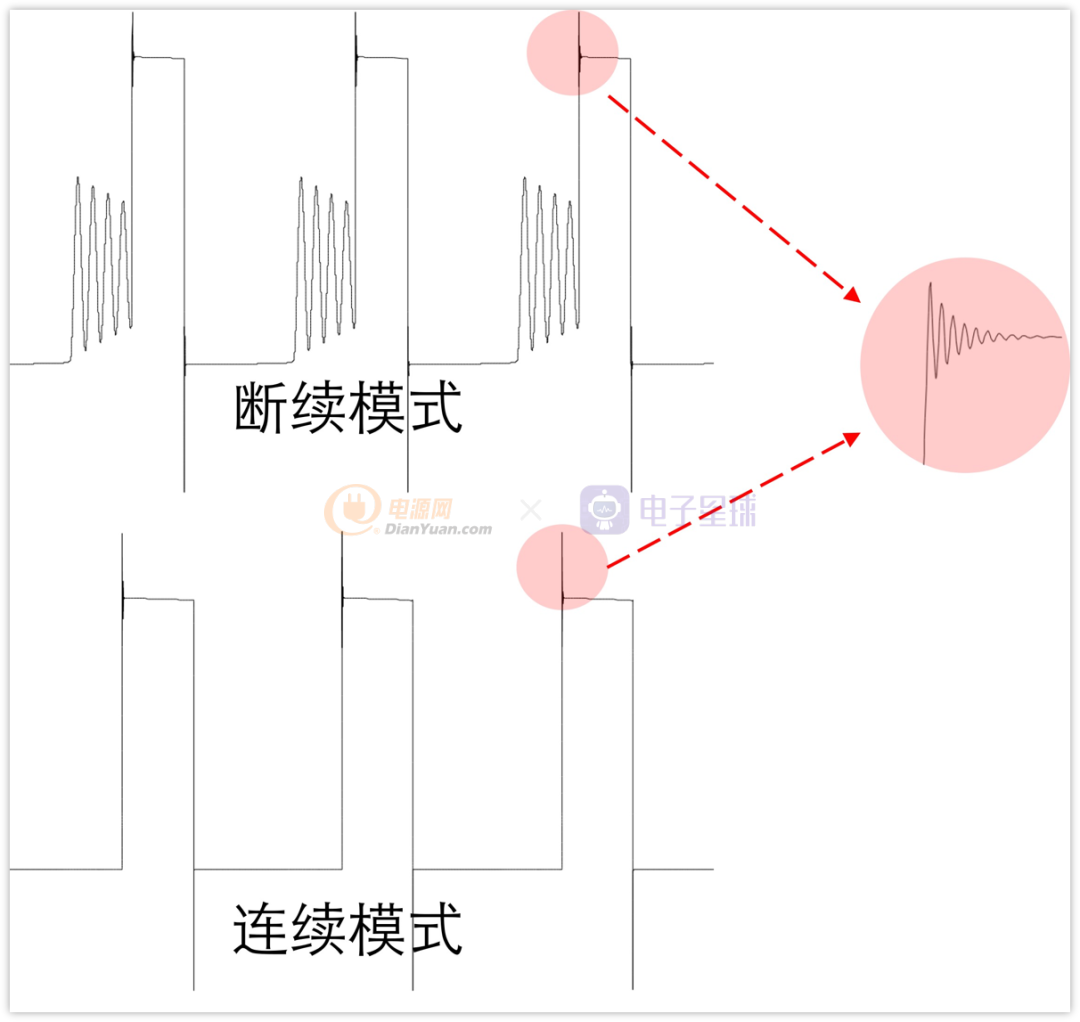
Buck电路电感前面的SW波形，想必大家都测量过，总的来说，无非下面两种：

不论是连续模式，还是断续模式，都会有上升尖峰或者是下降尖峰，无非是大小的问题。

如果我们拉开来看，尖峰可以看出来是一个振荡波形，频率很高。

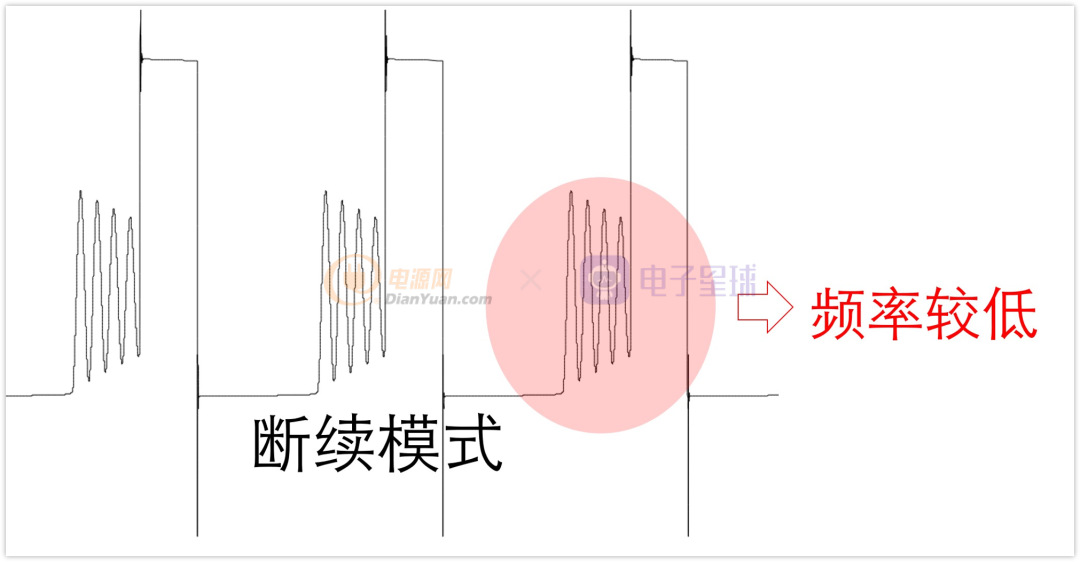
或者更明显的，断续模式中，在电感电流降低为0时就开始振荡，幅度不小，并且频率也不高。

对于新手来说，可能在心里打鼓：这个振荡莫不是有什么问题？

上面这些振荡，或是尖峰，要理解为什么长成这样？有没有问题？如何抑制？如果要详细了解来龙去脉，其实并不是很容易。

这些波形，本质上就是LC阻尼振荡，这一节我们先搞明白LC阻尼振荡的各种情况。

LC阻尼振荡

上面说的这些波形，产生的机理就是，在开关断开之前，电感或电容被充电。而在开关断开之后，电感或电容的能量需要释放，因此会找到电路中的寄生电容或是寄生电感，再结合电路中的等效电阻，组成了LC阻尼振荡。

Buck具体是如何构成LRC回路的，因为涉及到很多寄生参数，这个也不容易搞清楚，后面专门细说。

这节的主题就是LC阻尼振荡。

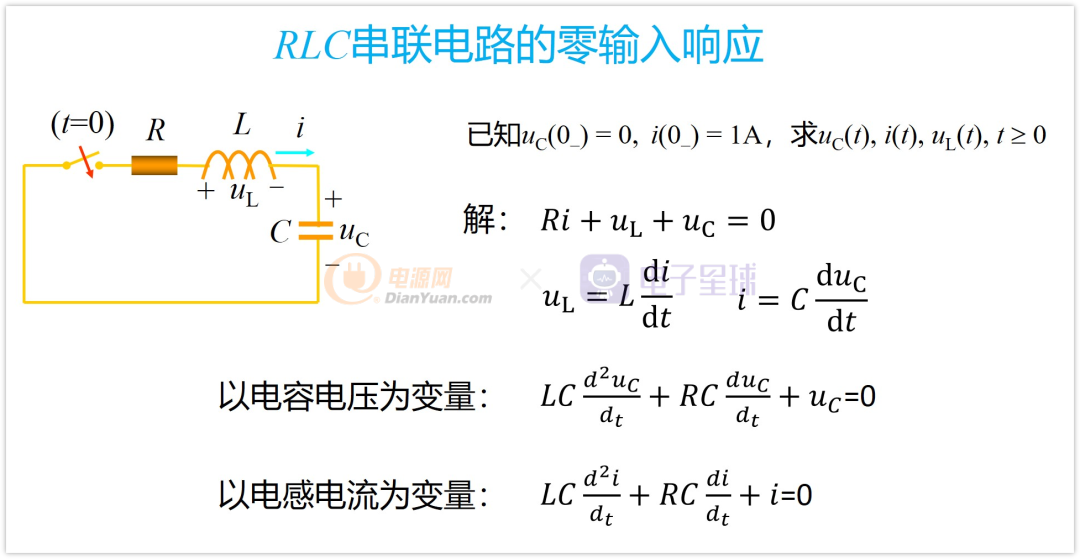
我们就以最简单的LRC串联电路来举例

这个电路其实在大学课程《电路分析》应该有学过（好像《信号与系统》这门课也有），就是一个二阶电路。

这个电路的波形分为四种情况，分别是：

最近get一个新技能，试着使用了一下LTspice仿真，感觉还不错，比Matlab方便吧。当然，也只能说明两个软件侧重点不一样吧，Matlab是数学工具，如果能用Matlab搞出下面的结果，理解肯定会更加的深入，但是难度更高吧。

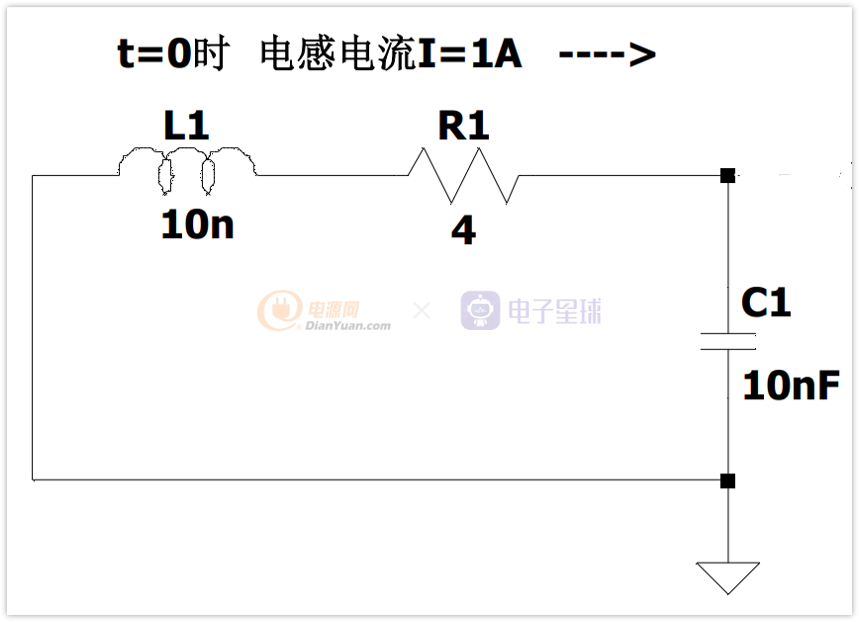
下面来看下我做的LTspice仿真：

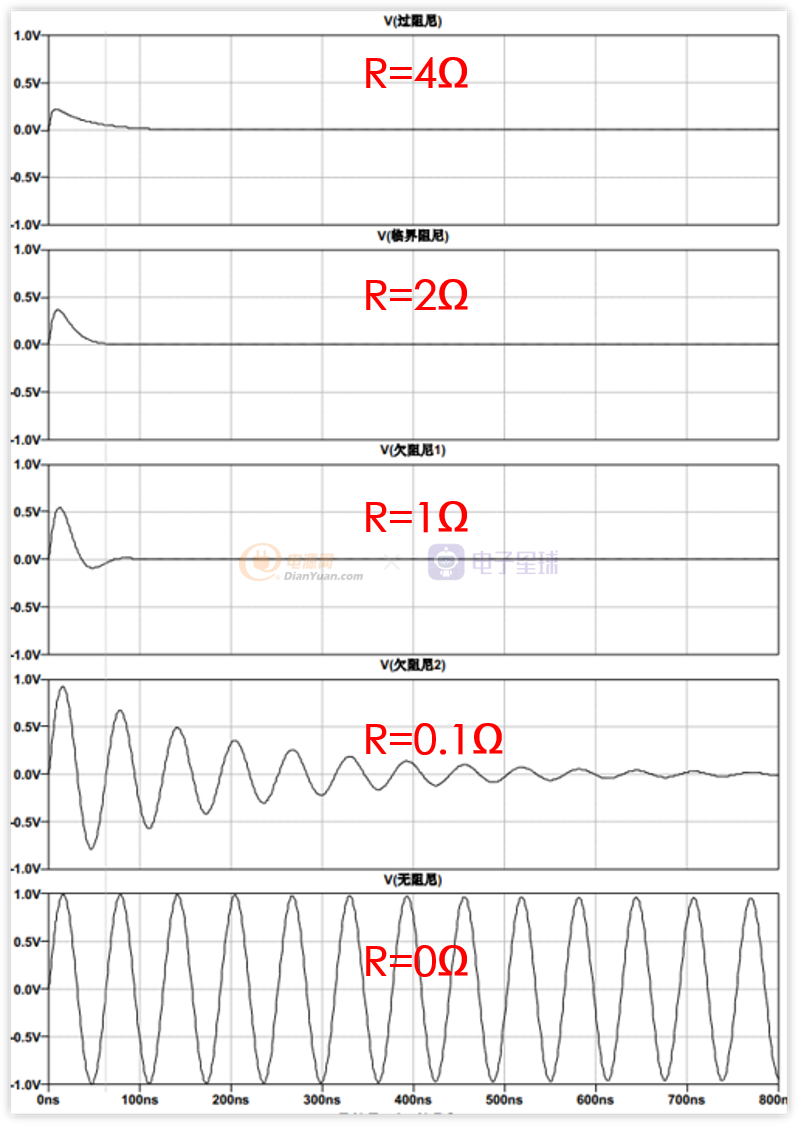
初始条件：L=10nH C=10nF 初始电感电流I=1A，电容电压为0V。

根据公式2(L/C)^0.5求得临界阻尼电阻R=2Ω。

下面我们只改变电阻R，让R=4Ω，2Ω，1Ω，0.1Ω，0Ω，分别来看看波形：

从上图我们可以得到振荡频率：

我们对比R=0.1和R=0的波形，可以看到，振荡的周期（两个波峰的时间差）是一样的，都是62.8ns左右，其实这就等于LC电路的谐振频率……

原文链接：
https://www.dianyuan.com/eestar/article-6417.html

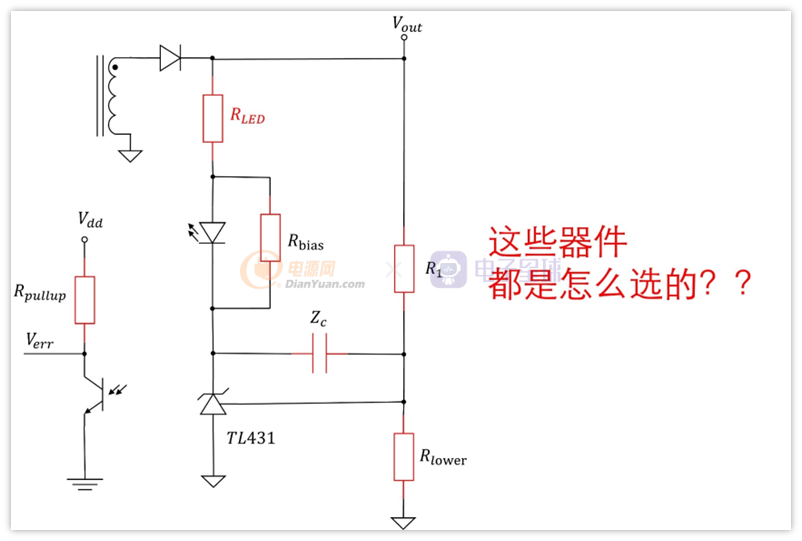
TL431电路的几个电阻的取值

从上一节我们知道，这里面一些电阻是跟环路相关的。不过在设计的时候，我们首先需要保证的不是环路，而是这个电路能不能工作起来，也就是说要给TL431合适的偏置。这个应该很容易理解吧，类似三极管放大，前提也是要给对直流偏置。

TL431工作前提条件

TL431工作主要有下面几点要求（以Ti的TL431C为例）：

1、Vka＞2.5V，Vka<36V

2、Ika>1mA，Ika<100mA，Iled<50mA

3、I分压电阻电流>100*Iref

那么这几个要求咋来的呢？

Ika，Vka可以直接从手册中看出来

不过手册中Vka只写了电压上限，那么我说的Vka＞2.5V怎么来的呢？

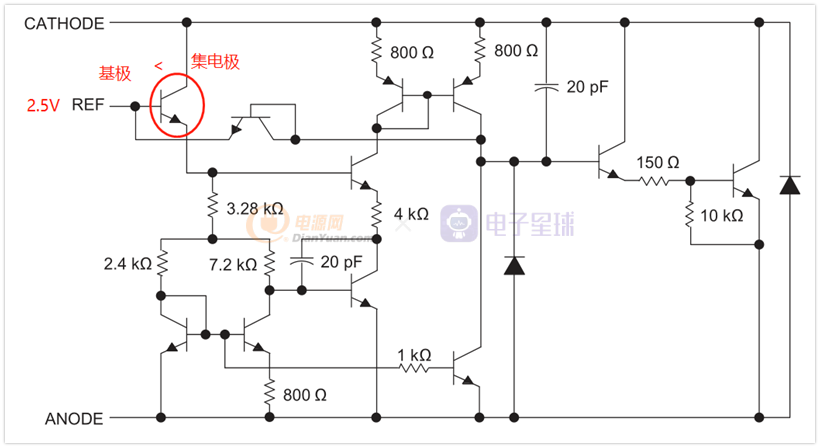
其实可以从TL431内部框图（规格书中有）中看出来，正常工作时，下面这个管子工作在了放大区，那么图中所示的三极管的集电极电压要比基极电压要大，即Cathode的电压要比Vref的电压要高，我们知道工作的时候Vref=2.5V，所以就有了Vka>2.5V。（Vka就是Cathode和Anode之间的电压）

Ika<100mA好理解，芯片电流大了，必然会发热，因此必须有个上限，像这种sot23封装的，电流上限一般也就在这个级别。

Ika>1mA，这是因为TL431工作时要满足静态偏置电流，这是其工作的条件。详细原因在我们前面的章节“TL431稳压是如何做到和温度基本”里面有说。

Iled<50mA，Iled指的是光耦的电流，以PC817为例，发光管最大电流为50mA。

那么I分压电阻电流>100*Iref呢？

一般我们输出电压是由分压比决定的，就是R1/Rlower，输出电压的计算公式是Vout=2.5V*（1+R1/RLower），可以看出，这是将Iref忽略掉了。要想能忽略掉Iref，那么就需要Iref<<Ilower，一般就是按照100倍来的，也就是Ilower>100*Ilower。

首先，看Rlower的大小

根据ILow＞100*Iref，一般普通Iref为2uA，因此Ilow>0.2mA。Rlower一头接GND，另外一头是Vref电压，为2.5V，所以Rlower两端电压是2.5V，电流是I=2.5V/Rlower>0.2mA，所以Rlower<12.5K。

不过我们需要知道，Rlower越小，那么电流也就越大，功耗越高，很多产品都对静态功耗有要求，因此Rlower需要尽量选大一点的阻值，所以常规都是10K左右的阻值。如果追求极致的功耗，希望进一步减小偏置电路的功耗，也可以选择静态电流小的TL431，比如我看到ti有Iref=0.03uA的低静态电流ATL431……

原文链接：
https://www.dianyuan.com/eestar/article-6014.html

一篇文章搞懂BUCK开关电源基础理论

介绍了BUCK拓扑降压的三种工作模式（CCM、BCM、DCM），介绍了伏秒平衡方程并通过伏秒平衡方程推导了输入输出电压与占空比的关系。本篇文章将首先介绍BUCK拓扑降压的设计指标-电流纹波率，并根据各项设计指标确定电感 开关等各个元器件的参数和选型。

电流纹波率

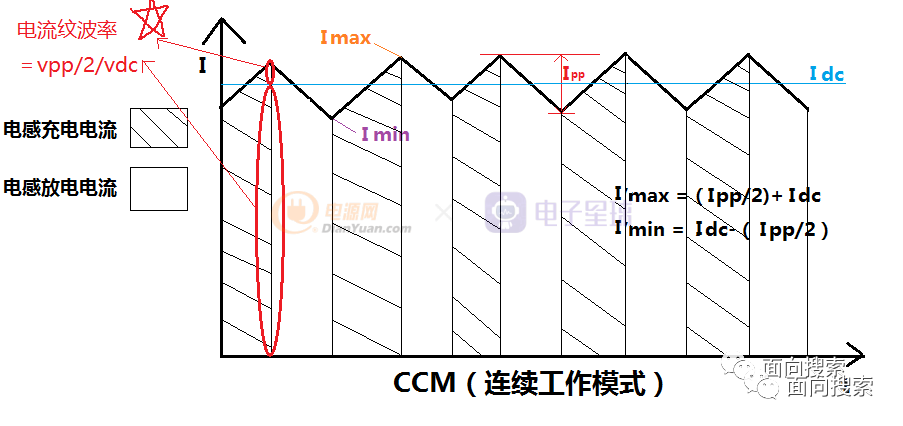
电流纹波率和大家熟知的电压纹波率是相对称的概念。电压纹波率是元器件两端的电压波动，而电流纹波率是流过元器件电流的波动，电感纹波率示意图如下图所示↓（电流纹波率＝vpp/2/vdc）。

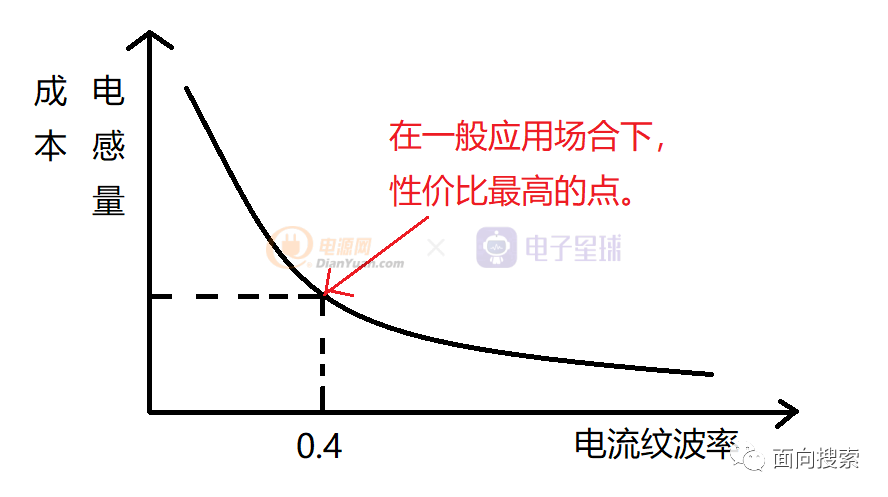
在BUCK的开关电源拓扑中，电感的电流纹波率是重要的设计指标，我们希望电流纹波率越接近于0越好，充放电越平稳，则电源的电压纹波 EMI等参数越好。但是如果想要电流纹波率越小，那么就需要电感的储能能力越强（电感值越大），大电感的缺点就是成本高 体积大 这是非常不利于我们的工程设计的， 下图为电感感值 成本与电流纹波率相对应的大致曲线↓

曲线是呈指数下降的，在实际的工程应用中，在没有特殊的要求下，我们认为取电流纹波率为0.4是从成本 电源稳定性等角度考虑比较高性价比的点，所以在后续的计算中我们将电流纹波率取0.4。

电感的选型

流过电感的平均电流、最小电流、最大电流。

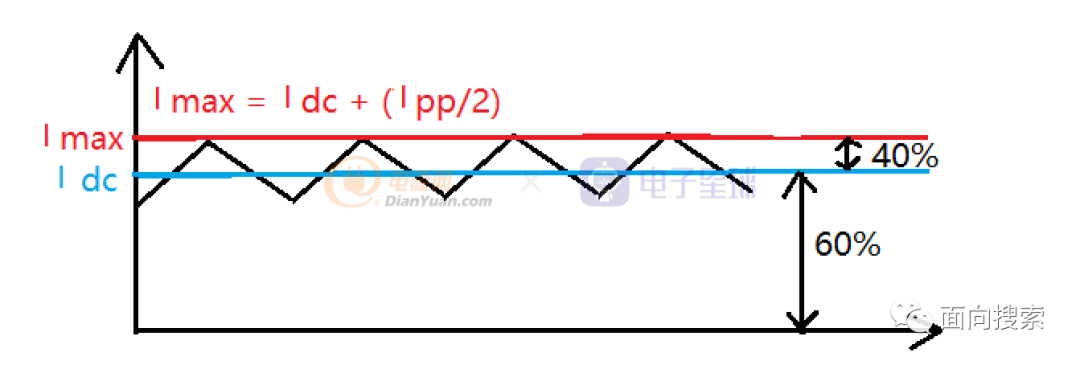
在确定CCM模式下的电流纹波率为0.4后，我们就可以画出电感的预期电流波形，如下图所示↓

流过电感的平均电流为Idc

流过电感的最大电流为Idc+(Ipp/2)

流过电感的最小电流为Idc-(Ipp/2)

在电感选型时要注意电感的最大承受电流和电感的饱和电流都要大于电感的平均电流，在工程应用下，我们通常会取 最大电流 * 1.2（少了不够，多了浪费 ）。

电感值的计算

在快速的开关下，开关的开通时间ton、开关的关断时间 toff 和 电流变化量△I都为较小的变化量。

则电感公式 U=L*di/dt 的另一种表达形式为：

Uon = L * (△Ion/Ton)；

Uoff = L * （ △Ioff / △Ton ）；

通过公式可知电流上升量和电流下降量为：

△Ion = (Uon * Ton) / L;

△Ioff = (Uoff * Toff) / L;

又知占空比公式为：

D=Ton/(Ton+Toff)=Ton/T=Ton*频率f;

通过公式可知电流上升量和电流下降量使用占空比进行表达为：

△Ion = (Uon * D ) / ( L * f );

△Ioff=[ Uoff*(1-D) ] / ( L * f );

电流纹波率公式为：

ρ = △Ion/Iout = △Ioff / Idc；（Iout 就是 Idc）

感量的计算公式，可通过电流上升量△Ion = (Uon * Ton) / L 计算，也可通过电流下降量△Ioff = (Uoff * Toff) / L 计算，下面就使用电流下降量公式做电感的计算（使用电流上升量公式做计算的结果也是相同的）。

公式△Ioff=[ Uoff*(1-D) ] / ( L * f )，使用电流纹波率的表达方式为：

ρ * Iout = [ Uoff*(1-D) ] / ( L * f );

则推导出电感计算公式：

L = [Uout*(1-D)]/(f*Iout*ρ)；(Uoff=Uout在上一篇文章中已经推导过)

在电感计算公式中，除了电感量L以外，其他的变量均已知则可求出电感具体值。

电感选型时的其他指标还包括：电感承受最大电流、电感饱和电流、电感的功率；通常这些参数我们要求留至少20%的余量。

开关的选型

在某些情况下我们所设计的BUCK降压电路的开关不会集成到开关芯片的内部，需要我们来进行选型，开关的选型最关键的参数有四个:

开关能承受的最大电压

开关能承受的最大电流

开关最高频率

开关能承受的最大功率

以上的参数应留取1-2倍的余量，后面还会更新文章实际搭建BUCK降压电路，再来详细的介绍这四个参数……

原文链接：
https://www.dianyuan.com/eestar/article-5821.html

开关电源环路稳定性分析(01)-Buck变换器

说到开关电源不得不提的就是开关的环路稳定性，但是这一块目前用的DC-DC芯片，很多厂家在芯片内部都已经做好了，所以对于使用的人来说，即使不太关注环路的稳定，按照手册中推荐的值设计产品也能正常使用。

当然，仅仅是按照手册中设计，但不清楚为什么要这样设计，让我一直感觉不踏实。我非常想知道为什么我这样设计环路就是稳定的，如果能像我用欧姆定律一样，拿个万用表一测就知道，至少是这样的程度，才让我感觉自己做的东西是可靠的！

因此，工作这么久，我一直对开关电源环路这块的知识点有些不放心，就像别人问你哪一块学得最好时，人家问会开关电源吗？我想，如果我直接说我会，我感觉比较心虚，比如设计的电源增益是多少，相位裕量是多少？这些我可能都说不清楚。

因此，我始终都认为，要把开关电源稳定性好好研究一下。

言归正传，今天我们开始开关电源环路稳定性的第一讲。

为了大家能都能理解这个晦涩难懂的知识模块，会从最基本的电源理论开始，再到传递函数，波特图，环路稳定性判据，环路补偿模型这样慢慢的深入。

1. 开关电源系统

开关电源，从名字就知道这个系统有开关，而在电子中最常用的开关是什么？三极管，MOS管，晶闸管。的确在不同的电源中，这三种器件都有使用。在理解开关电源环路稳定性时，我们要建立闭环的概念，也就是存在反馈。如果没有反馈，那系统就是开环的。

比如，我们坐公交的时候经常会听到“您已超速，请减速”，司机就会将车子速度降低，这就是一个典型的闭环系统，如果没有速率的监测，那司机是无法准确知道当前的速度以及是否存在超速。再比如夏天开空调，热的时候，你会开到16°，冷的时候，你又会调到25°，你感觉到热或者冷，就是反馈。

根据上面的分析，在理解开关电源环路稳定的时候，也可以借助一些能量传递模型来理解环路的稳定，这个在后面的文章会有涉及。

2. DC-DC拓扑

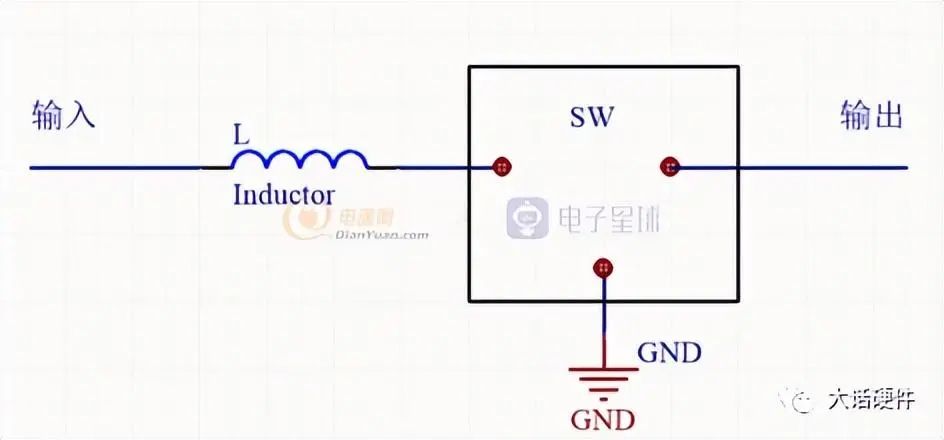
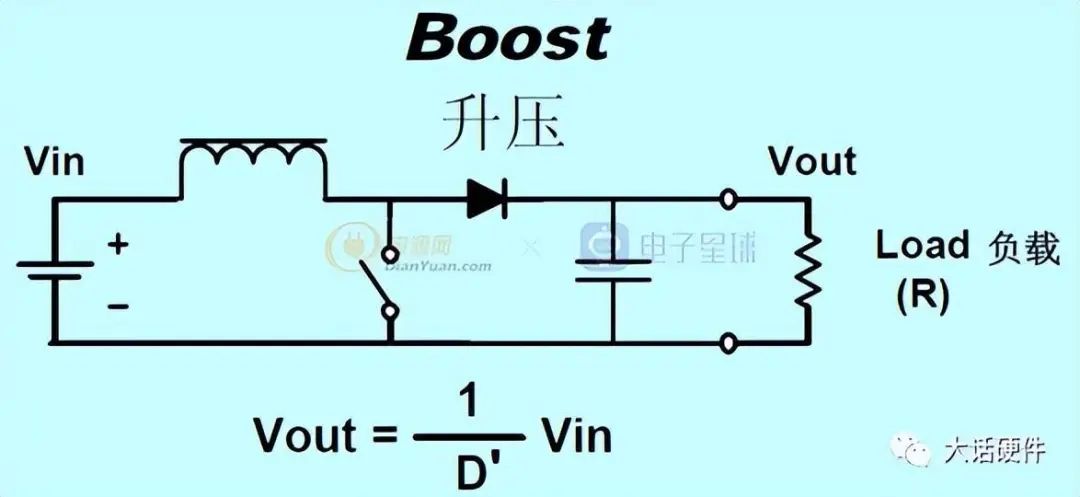
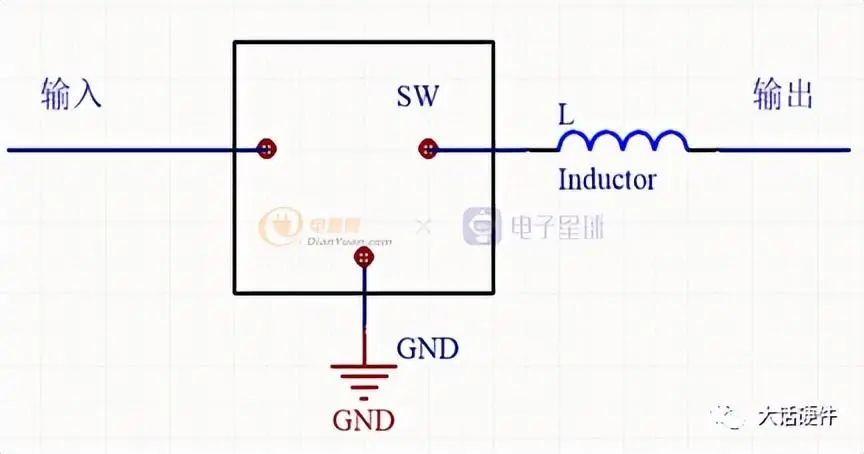
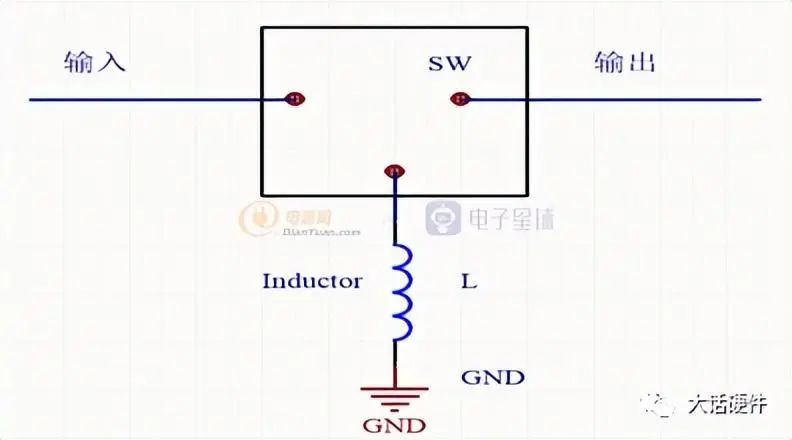
开关电源的种类很多，隔离的非隔离的，降压的，升压的，升降压的。为了降低分析的难度，主要关注boost，buck，buck-boost这三种。而这三种拓扑在区分的时候，可以以电感为中心，电感接输入，输出，和地形成了这三种拓扑。

Boost拓扑

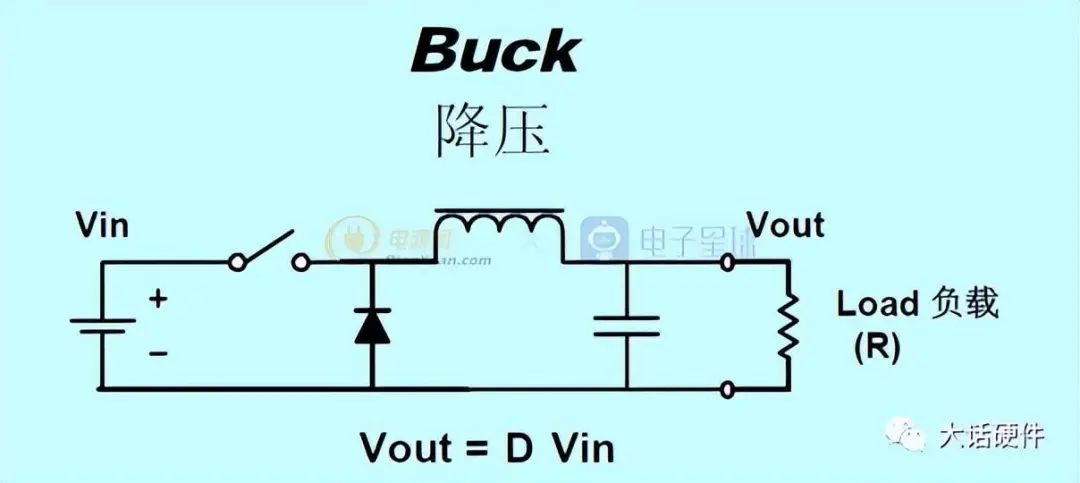
Buck拓扑

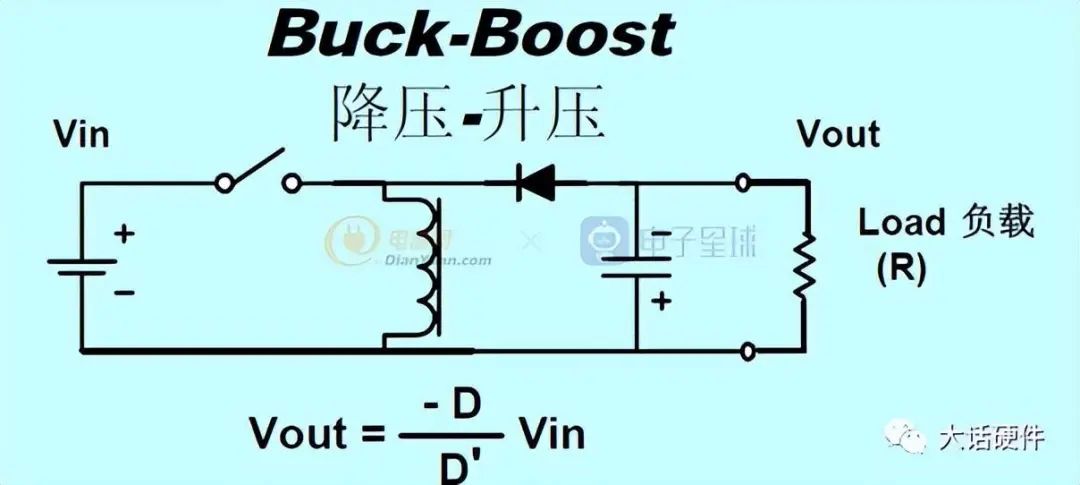
Buck-Boost拓扑

3. Buck变换器工作原理

在分析Buck工作原理时，其实我们都是基于稳态，甚至是连续导通模式(CCM)，相比断续模式来说，从连续导通模式甚至是临界连续模式入手，是比较简单而且非常有效的一种手段。

下面以CCM模式，来分析开关导通时和闭合时开关电源输入输出之间的关系……

原文链接：
https://www.dianyuan.com/eestar/article-5812.html

开关电源中的斜坡补偿

在开关电源DCDC变换器中，在采用电压模式控制中，由输出电压反馈与电源芯片内部锯齿波载波信号比较产生PWM波进而控制开关管的占空比来实现输出电压的控制，这种控制方式并不需要考虑斜坡补偿，而在电流模式控制中，控制环路中存在电压控制外环和电流控制内环两个反馈环。其中的电流环为流过开关管的斜坡电流信号，它经过采样电阻转换为斜坡电压信号，斜坡电压信号和反馈比较电压一起决定PWM的占空比。

1.为什么需要斜率补偿

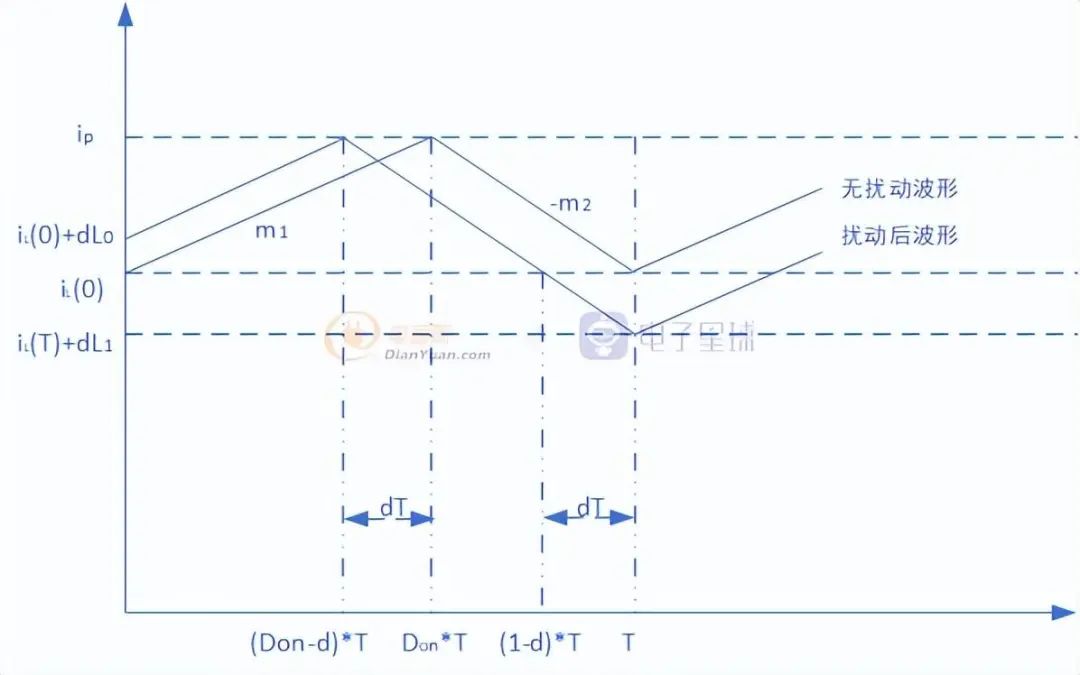
下面以Buck峰值电流控制为例，分析斜坡补偿的原理：图1中正常无扰动电感电流波形，电流的上升斜率为m1，下降斜率为-m2，m1和m2的值和电路拓扑有关，以Buck变换器为例，电感的上升斜率m1=(Vin-Vout)/L,下降斜率-m2=-Vout/L。

图 1 电感电流波形

无扰动情况下，在电路工作的0~Don*T时间内，开关管导通，二极管截止，电感电流线性增加，在Don*T时刻，电流达到峰值,电感电流为

在Don*T~T时间内，开关管关断，电感电流通过二极管续流，电感电流线性下降，在T时刻，电感电流为

当电路工作在稳定状态下，

因此，在理想状态下

图1中电感电流不存在扰动情况下的电流变化的波形：在没有扰动时，电感电流在开关周期初始时电流为iL(0)；在Don*T时，电感电流达到最大值ip；在T时刻，电感电流为iL(T)。

图1中电感电流在存在扰动下的电流波形：在t=0时刻存在一扰动dL，其值在初始时变为iL(0)=iL0+dL0,于是Buck电路的占空比由扰动情况下的Don变为Don-d,在t=(Don-d)*T,电感电流达到峰值；当t=T时，电感电流下降到iL(T)-dL1,电感电流在一个周期中的初始和结束时刻电流值不等，

由前面的分析可得

同理可得

结合前面的公式可得

上式表明每个周期结束时的电感电流扰动量等于周期开始时刻的电感电流扰动量与-m2/m1的乘积，可以得到……